
Balok adalah salah satu bentuk bangun ruang tiga dimensi yang memiliki sifat khusus. Bangun ini terdiri dari rusuk, sisi, dan titik sudut yang saling berhubungan. Salah satu ciri khas balok adalah adanya sisi-sisi yang saling berhadapan dengan ukuran yang sama. Benda-benda sehari-hari yang berbentuk balok antara lain kotak tisu, tempat pensil, lemari, serta kotak susu. Untuk memahami lebih dalam tentang balok, kita perlu mengetahui ciri-ciri, rumus luas permukaan, serta cara menghitungnya.
Ciri-Ciri Balok
Balok memiliki beberapa ciri yang dapat membantu dalam memahami struktur dan sifat-sifatnya. Berikut beberapa ciri utama balok:
- Memiliki 6 sisi yang masing-masing berbentuk persegi panjang.
- Terdapat 12 rusuk yang terbagi menjadi 3 pasang rusuk yang sama panjang.
- Setiap sisi balok memiliki pasangan yang sama ukurannya.
- Memiliki 8 titik sudut yang semuanya merupakan sudut siku-siku.
- Terdapat 4 diagonal ruang dan 12 diagonal bidang.
- Jaring-jaring balok terdiri dari 6 buah persegi panjang yang saling terhubung.
Dengan memahami ciri-ciri ini, kita akan lebih mudah dalam menggambar atau menghitung berbagai parameter balok.
Rumus Luas Permukaan Balok
Luas permukaan balok didefinisikan sebagai jumlah seluruh luas dari semua sisi yang ada pada balok. Rumus umum untuk menghitung luas permukaan balok adalah sebagai berikut:
$$ L = 2 imes (p imes l + p imes t + l imes t) $$
Atau bisa ditulis juga sebagai:
$$ L = 2(pl + pt + lt) $$
Keterangan: - $ p $: panjang balok - $ l $: lebar balok - $ t $: tinggi balok
Rumus ini berasal dari penjumlahan luas semua sisi balok. Karena balok memiliki 6 sisi dengan dua pasang sisi yang sama, maka rumus tersebut dirancang agar tidak perlu menghitung setiap sisi secara terpisah.
Pembuktian Rumus Luas Balok
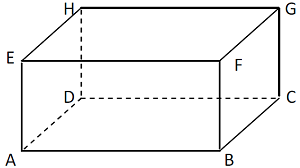
Untuk memperjelas bagaimana rumus di atas diperoleh, mari kita lihat contoh pembuktian menggunakan nama balok ABCD.EFGH. Sisi-sisi balok ini meliputi:
- ABFE (sisi depan)
- DCGH (sisi belakang)
- EFGH (sisi atas)
- ABCD (sisi bawah)
- BCGF (sisi kanan)
- ADHE (sisi kiri)
Dari sini, kita tahu bahwa sisi depan dan belakang memiliki luas yang sama, demikian pula dengan sisi atas dan bawah, serta sisi kanan dan kiri. Maka:
$$ L_{ABCD.EFGH} = 2 imes L_{ABFE} + 2 imes L_{EFGH} + 2 imes L_{BCGF} $$
Jika kita substitusi nilai panjang, lebar, dan tinggi ke dalam rumus, maka:
$$ L = 2(pl + pt + lt) $$
Contoh Soal Luas Balok
Untuk lebih memahami penggunaan rumus, mari kita lihat contoh soal berikut:
Sebuah tempat pensil berbentuk balok memiliki ukuran panjang 28 cm, lebar 16 cm, dan tinggi 20 cm. Hitunglah luas permukaan balok tersebut!
Diketahui:
- Panjang ($ p $) = 28 cm
- Lebar ($ l $) = 16 cm
- Tinggi ($ t $) = 20 cm
Penyelesaian: $$ L = 2 imes (pl + pt + lt) $$ $$ L = 2 imes ((28 imes 16) + (28 imes 20) + (16 imes 20)) $$ $$ L = 2 imes (448 + 560 + 320) $$ $$ L = 2 imes 1328 $$ $$ L = 2656 , ext{cm}^2 $$
Jadi, luas permukaan balok tersebut adalah 2656 cm².
Kesimpulan
Balok merupakan bangun ruang yang sangat umum ditemukan dalam kehidupan sehari-hari. Dengan memahami ciri-ciri, rumus luas permukaan, serta cara menghitungnya, kita dapat lebih mudah dalam mengerjakan berbagai soal terkait balok. Latihan terus-menerus akan membantu meningkatkan pemahaman dan kecepatan dalam menghitung.




















Komentar
Tuliskan Komentar Anda!